Common Steps on a Machine Learning Project 23 Feb 2019
A sequence of common steps when working with a machine learning project
Using the house sales prediction dataset: https://www.kaggle.com/harlfoxem/housesalesprediction
# Common imports
import numpy as np
import os
# Import and settings for plotings figures
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
Get the Data
# Once the data have been downloaded and stored at ./datasets/housesales
house_sales_path = os.path.join("datasets", "housesales")
# Import panda
import pandas as pd
# Create a function to load the dataset into a panda object
def load_house_sales(path=house_sales_path):
csv_path = os.path.join(path, "kc_house_data.csv")
return pd.read_csv(csv_path)
# Call our function to load the dataset
housesales = load_house_sales()
# This step is done for simulating that we have same NaN values.
# In a real project, it does need to be done
shuffled_indices = np.random.permutation(len(housesales))
na_size = int(len(housesales) * 2 / 1000)
na_indices = shuffled_indices[:na_size]
housesales.loc[na_indices, 'sqft_living'] = np.nan
# View null values
housesales[housesales.isnull().any(axis=1)].head(5)
| id | date | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | ... | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 293 | 6073240060 | 20141002T000000 | 580000.0 | 4 | 3.00 | NaN | 11060 | 2.0 | 0 | 0 | ... | 8 | 2270 | 1010 | 1986 | 0 | 98056 | 47.5399 | -122.181 | 2320 | 11004 |
| 451 | 3775300030 | 20141231T000000 | 333500.0 | 3 | 1.75 | NaN | 9732 | 1.0 | 0 | 0 | ... | 7 | 1220 | 0 | 1965 | 0 | 98011 | 47.7736 | -122.214 | 1630 | 10007 |
| 1595 | 5315100737 | 20140528T000000 | 900000.0 | 6 | 2.75 | NaN | 24773 | 1.5 | 0 | 0 | ... | 9 | 2300 | 0 | 1950 | 1985 | 98040 | 47.5833 | -122.242 | 2720 | 11740 |
| 1806 | 8079100370 | 20141107T000000 | 574000.0 | 3 | 2.00 | NaN | 7000 | 1.0 | 0 | 0 | ... | 9 | 2060 | 0 | 1988 | 0 | 98029 | 47.5644 | -122.012 | 2110 | 7000 |
| 2104 | 4142450510 | 20140723T000000 | 310000.0 | 3 | 2.50 | NaN | 3600 | 2.0 | 0 | 0 | ... | 7 | 1990 | 0 | 2004 | 0 | 98038 | 47.3841 | -122.041 | 1790 | 3600 |
5 rows × 21 columns
# This step is done for simulating that we have a category column
# In a real project, it does need to be done
shuffled_indices = np.random.permutation(len(housesales))
cats = ['A', 'B', 'C', 'D', 'E']
cat_size = int(len(housesales) / 5)
rem = len(housesales) % 5
for i in range(5):
plus = 0
if i == 4:
plus = rem
indices = shuffled_indices[i*cat_size:((i+1)*cat_size + plus)]
housesales.loc[indices, "new_cat"] = cats[i]
A quick look at the data
# Explore first rows of our dataset
housesales.head()
| id | date | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | ... | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | new_cat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7129300520 | 20141013T000000 | 221900.0 | 3 | 1.00 | 1180.0 | 5650 | 1.0 | 0 | 0 | ... | 1180 | 0 | 1955 | 0 | 98178 | 47.5112 | -122.257 | 1340 | 5650 | D |
| 1 | 6414100192 | 20141209T000000 | 538000.0 | 3 | 2.25 | 2570.0 | 7242 | 2.0 | 0 | 0 | ... | 2170 | 400 | 1951 | 1991 | 98125 | 47.7210 | -122.319 | 1690 | 7639 | D |
| 2 | 5631500400 | 20150225T000000 | 180000.0 | 2 | 1.00 | 770.0 | 10000 | 1.0 | 0 | 0 | ... | 770 | 0 | 1933 | 0 | 98028 | 47.7379 | -122.233 | 2720 | 8062 | A |
| 3 | 2487200875 | 20141209T000000 | 604000.0 | 4 | 3.00 | 1960.0 | 5000 | 1.0 | 0 | 0 | ... | 1050 | 910 | 1965 | 0 | 98136 | 47.5208 | -122.393 | 1360 | 5000 | A |
| 4 | 1954400510 | 20150218T000000 | 510000.0 | 3 | 2.00 | 1680.0 | 8080 | 1.0 | 0 | 0 | ... | 1680 | 0 | 1987 | 0 | 98074 | 47.6168 | -122.045 | 1800 | 7503 | B |
5 rows × 22 columns
# Show info of our dataset
housesales.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 21613 entries, 0 to 21612
Data columns (total 22 columns):
id 21613 non-null int64
date 21613 non-null object
price 21613 non-null float64
bedrooms 21613 non-null int64
bathrooms 21613 non-null float64
sqft_living 21570 non-null float64
sqft_lot 21613 non-null int64
floors 21613 non-null float64
waterfront 21613 non-null int64
view 21613 non-null int64
condition 21613 non-null int64
grade 21613 non-null int64
sqft_above 21613 non-null int64
sqft_basement 21613 non-null int64
yr_built 21613 non-null int64
yr_renovated 21613 non-null int64
zipcode 21613 non-null int64
lat 21613 non-null float64
long 21613 non-null float64
sqft_living15 21613 non-null int64
sqft_lot15 21613 non-null int64
new_cat 21613 non-null object
dtypes: float64(6), int64(14), object(2)
memory usage: 3.6+ MB
# Count values for discrete columns
housesales["grade"].value_counts()
7 8981
8 6068
9 2615
6 2038
10 1134
11 399
5 242
12 90
4 29
13 13
3 3
1 1
Name: grade, dtype: int64
# Obtain statistics for numerical columns
housesales.describe()
| id | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 2.161300e+04 | 2.161300e+04 | 21613.000000 | 21613.000000 | 21570.000000 | 2.161300e+04 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 | 21613.000000 |
| mean | 4.580302e+09 | 5.400881e+05 | 3.370842 | 2.114757 | 2079.939917 | 1.510697e+04 | 1.494309 | 0.007542 | 0.234303 | 3.409430 | 7.656873 | 1788.390691 | 291.509045 | 1971.005136 | 84.402258 | 98077.939805 | 47.560053 | -122.213896 | 1986.552492 | 12768.455652 |
| std | 2.876566e+09 | 3.671272e+05 | 0.930062 | 0.770163 | 918.688179 | 4.142051e+04 | 0.539989 | 0.086517 | 0.766318 | 0.650743 | 1.175459 | 828.090978 | 442.575043 | 29.373411 | 401.679240 | 53.505026 | 0.138564 | 0.140828 | 685.391304 | 27304.179631 |
| min | 1.000102e+06 | 7.500000e+04 | 0.000000 | 0.000000 | 290.000000 | 5.200000e+02 | 1.000000 | 0.000000 | 0.000000 | 1.000000 | 1.000000 | 290.000000 | 0.000000 | 1900.000000 | 0.000000 | 98001.000000 | 47.155900 | -122.519000 | 399.000000 | 651.000000 |
| 25% | 2.123049e+09 | 3.219500e+05 | 3.000000 | 1.750000 | 1425.500000 | 5.040000e+03 | 1.000000 | 0.000000 | 0.000000 | 3.000000 | 7.000000 | 1190.000000 | 0.000000 | 1951.000000 | 0.000000 | 98033.000000 | 47.471000 | -122.328000 | 1490.000000 | 5100.000000 |
| 50% | 3.904930e+09 | 4.500000e+05 | 3.000000 | 2.250000 | 1910.000000 | 7.618000e+03 | 1.500000 | 0.000000 | 0.000000 | 3.000000 | 7.000000 | 1560.000000 | 0.000000 | 1975.000000 | 0.000000 | 98065.000000 | 47.571800 | -122.230000 | 1840.000000 | 7620.000000 |
| 75% | 7.308900e+09 | 6.450000e+05 | 4.000000 | 2.500000 | 2550.000000 | 1.068800e+04 | 2.000000 | 0.000000 | 0.000000 | 4.000000 | 8.000000 | 2210.000000 | 560.000000 | 1997.000000 | 0.000000 | 98118.000000 | 47.678000 | -122.125000 | 2360.000000 | 10083.000000 |
| max | 9.900000e+09 | 7.700000e+06 | 33.000000 | 8.000000 | 13540.000000 | 1.651359e+06 | 3.500000 | 1.000000 | 4.000000 | 5.000000 | 13.000000 | 9410.000000 | 4820.000000 | 2015.000000 | 2015.000000 | 98199.000000 | 47.777600 | -121.315000 | 6210.000000 | 871200.000000 |
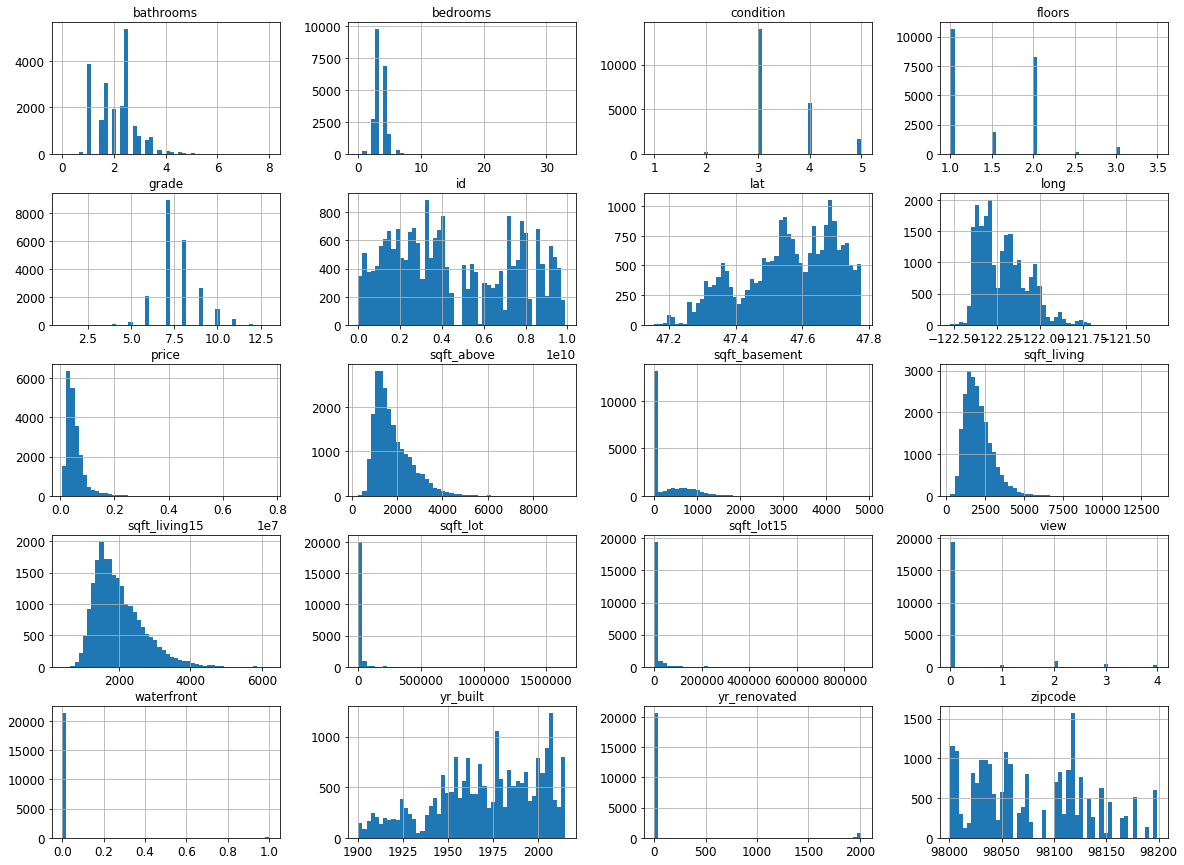
# Plot the histogram for each numerical value
import matplotlib.pyplot as plt
housesales.hist(bins=50, figsize=(20,15))
plt.show()
Create the test set
# Make this notebook's output identical at every run
np.random.seed(10)
# Split the data into train and test dataset by using our own function
# For illustration only. Sklearn has train_test_split()
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housesales, 0.2)
print(len(train_set), "train +", len(test_set), "test")
17291 train + 4322 test
# Split the data into train and test dataset by using sklearn tools
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housesales, test_size=0.2, random_state=10)
print(len(train_set), "train +", len(test_set), "test")
17290 train + 4323 test
Data Discovering and Visualization
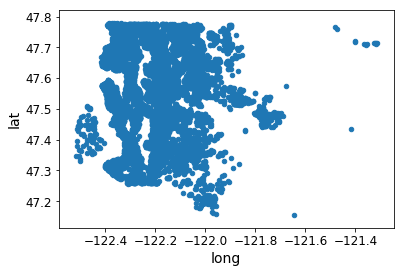
# Plot data points by using their latitute and longitude
housesales = train_set.copy()
housesales.plot(kind="scatter", x="long", y="lat")
<matplotlib.axes._subplots.AxesSubplot at 0x3ab4a4ae80>
# Since data belongs to King County, USA, we can obtain its map
# Load and plot that map
img_path = os.path.join("datasets", "housesales", "King_County_Washington.png")
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img=mpimg.imread(img_path)
imgplot = plt.imshow(img)
plt.show()
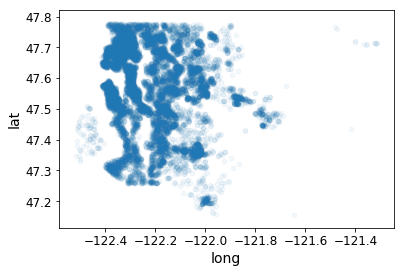
# Add alpha(transparency) to see density of data points
housesales.plot(kind="scatter", x="long", y="lat", alpha=0.05)
<matplotlib.axes._subplots.AxesSubplot at 0x3ab20d0f98>
# Use color and mark size to point out price and grade features
housesales.plot(kind="scatter", x="long", y="lat", alpha=0.3,
s=housesales["grade"]*10, label="grade", figsize=(12,8),
c="price", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False
)
plt.legend()
<matplotlib.legend.Legend at 0x3ab4bdd2b0>

# Integrate its map to the previous plot
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
housesales.plot(kind="scatter", x="long", y="lat", alpha=0.2,
s=housesales["grade"]*10, label="grade", figsize=(16,8),
c="price", cmap=plt.get_cmap("jet"), colorbar=False,
sharex=False
)
plt.ylabel("Latitude", fontsize=14)
plt.xlabel("Longitude", fontsize=14)
king_img = mpimg.imread(img_path)
plt.imshow(king_img, extent=[-122.54, -120.80, 47.04, 47.85], alpha=0.4,
cmap=plt.get_cmap("jet"))
prices = housesales["price"]
tick_values = np.linspace(prices.min(), prices.max(), 11)
cbar = plt.colorbar()
cbar.ax.set_yticklabels(["$%dk"%(round(v/1000)) for v in tick_values], fontsize=14)
cbar.set_label('Price', fontsize=16)
plt.legend()
<matplotlib.legend.Legend at 0x3ab7164128>
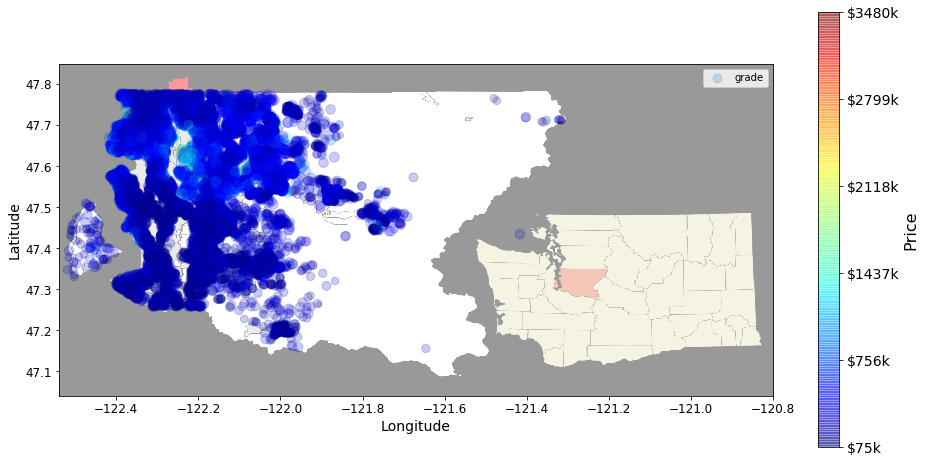
Looking for correlations
# Generate the correlation matrix
corr_matrix = housesales.corr()
# Show features more correlated to the 'price' feature
corr_matrix['price'].sort_values(ascending=False)
price 1.000000
sqft_living 0.699090
grade 0.675100
sqft_above 0.605499
sqft_living15 0.596289
bathrooms 0.523657
view 0.395379
sqft_basement 0.315418
lat 0.309859
bedrooms 0.302944
waterfront 0.257969
floors 0.252762
yr_renovated 0.115392
sqft_lot 0.091601
sqft_lot15 0.082624
yr_built 0.060613
condition 0.035486
long 0.022572
id -0.013927
zipcode -0.057404
Name: price, dtype: float64
# Plot scatter plots among the most correlated features
# For the main diagonal, pandas displays a histogram instead of straight line(variable against itself)
from pandas.plotting import scatter_matrix
attributes = ["price", "sqft_living", "grade","sqft_above", "bathrooms"]
fig = scatter_matrix(housesales[attributes], figsize=(12, 8))
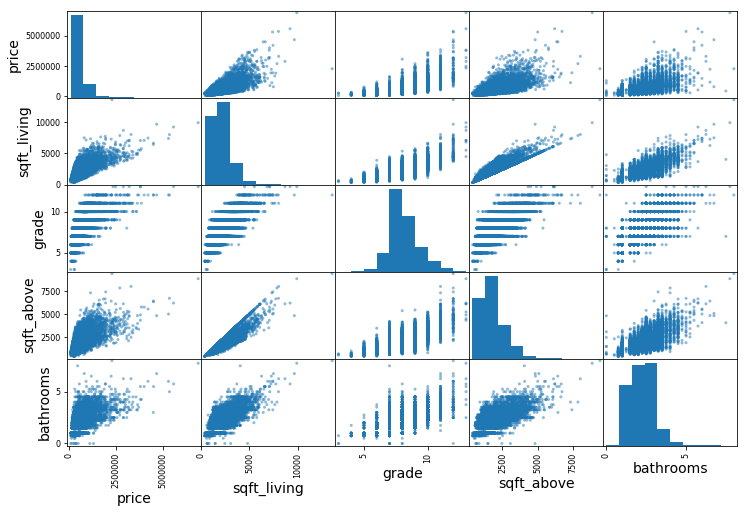
# Plot the scatter plot between two especific features
housesales.plot(kind="scatter", x="sqft_living", y="price", alpha=0.1)
plt.axis([0, 7000, 0, 2000000])
[0, 7000, 0, 2000000]
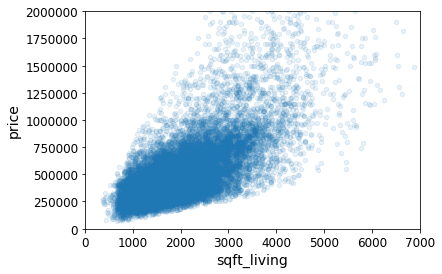
Prepare Data for Machine Learning
# drop labels for training set
housesales = train_set.drop("price", axis=1)
# Assign labels to a new variable
housesales_labels = train_set["price"].copy()
Data Cleaning
# Look at incomplete features
incomplete_rows = housesales[housesales.isnull().any(axis=1)]
incomplete_rows.head(5)
| id | date | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | ... | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | new_cat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7517 | 2223059052 | 20140529T000000 | 4 | 2.00 | NaN | 6375 | 2.0 | 0 | 0 | 3 | ... | 1530 | 0 | 1942 | 1983 | 98058 | 47.4692 | -122.162 | 1500 | 8712 | B |
| 5711 | 3222069153 | 20141024T000000 | 3 | 2.25 | NaN | 17235 | 1.0 | 0 | 0 | 4 | ... | 1440 | 280 | 1974 | 0 | 98042 | 47.3438 | -122.073 | 1990 | 35048 | C |
| 20979 | 9895000040 | 20140703T000000 | 2 | 1.75 | NaN | 1005 | 1.5 | 0 | 0 | 3 | ... | 900 | 510 | 2011 | 0 | 98027 | 47.5446 | -122.018 | 1440 | 1188 | D |
| 19431 | 4022900652 | 20141118T000000 | 5 | 3.25 | NaN | 20790 | 1.0 | 0 | 0 | 4 | ... | 1800 | 1060 | 1965 | 0 | 98155 | 47.7757 | -122.295 | 1920 | 9612 | E |
| 10994 | 7309100270 | 20140626T000000 | 4 | 1.75 | NaN | 6975 | 1.0 | 0 | 0 | 3 | ... | 1420 | 300 | 1975 | 0 | 98052 | 47.6506 | -122.121 | 2210 | 7875 | D |
5 rows × 21 columns
# option 1: Drop rows containing NaN values
incomplete_rows.dropna(subset=["sqft_living"])
| id | date | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | ... | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | new_cat |
|---|
0 rows × 21 columns
# option 2: Drop feature containing NaN values
incomplete_rows.drop("sqft_living", axis=1).head()
| id | date | bedrooms | bathrooms | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | new_cat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7517 | 2223059052 | 20140529T000000 | 4 | 2.00 | 6375 | 2.0 | 0 | 0 | 3 | 7 | 1530 | 0 | 1942 | 1983 | 98058 | 47.4692 | -122.162 | 1500 | 8712 | B |
| 5711 | 3222069153 | 20141024T000000 | 3 | 2.25 | 17235 | 1.0 | 0 | 0 | 4 | 7 | 1440 | 280 | 1974 | 0 | 98042 | 47.3438 | -122.073 | 1990 | 35048 | C |
| 20979 | 9895000040 | 20140703T000000 | 2 | 1.75 | 1005 | 1.5 | 0 | 0 | 3 | 9 | 900 | 510 | 2011 | 0 | 98027 | 47.5446 | -122.018 | 1440 | 1188 | D |
| 19431 | 4022900652 | 20141118T000000 | 5 | 3.25 | 20790 | 1.0 | 0 | 0 | 4 | 7 | 1800 | 1060 | 1965 | 0 | 98155 | 47.7757 | -122.295 | 1920 | 9612 | E |
| 10994 | 7309100270 | 20140626T000000 | 4 | 1.75 | 6975 | 1.0 | 0 | 0 | 3 | 8 | 1420 | 300 | 1975 | 0 | 98052 | 47.6506 | -122.121 | 2210 | 7875 | D |
# option 3: Fill out features containing NaN values with some criteria(i.e. median)
median = housesales["sqft_living"].median()
incomplete_rows["sqft_living"].fillna(median, inplace=True)
incomplete_rows.head(5)
| id | date | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | ... | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | new_cat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7517 | 2223059052 | 20140529T000000 | 4 | 2.00 | 1910.0 | 6375 | 2.0 | 0 | 0 | 3 | ... | 1530 | 0 | 1942 | 1983 | 98058 | 47.4692 | -122.162 | 1500 | 8712 | B |
| 5711 | 3222069153 | 20141024T000000 | 3 | 2.25 | 1910.0 | 17235 | 1.0 | 0 | 0 | 4 | ... | 1440 | 280 | 1974 | 0 | 98042 | 47.3438 | -122.073 | 1990 | 35048 | C |
| 20979 | 9895000040 | 20140703T000000 | 2 | 1.75 | 1910.0 | 1005 | 1.5 | 0 | 0 | 3 | ... | 900 | 510 | 2011 | 0 | 98027 | 47.5446 | -122.018 | 1440 | 1188 | D |
| 19431 | 4022900652 | 20141118T000000 | 5 | 3.25 | 1910.0 | 20790 | 1.0 | 0 | 0 | 4 | ... | 1800 | 1060 | 1965 | 0 | 98155 | 47.7757 | -122.295 | 1920 | 9612 | E |
| 10994 | 7309100270 | 20140626T000000 | 4 | 1.75 | 1910.0 | 6975 | 1.0 | 0 | 0 | 3 | ... | 1420 | 300 | 1975 | 0 | 98052 | 47.6506 | -122.121 | 2210 | 7875 | D |
5 rows × 21 columns
# Option 3B: Fill out features containing NaN values by using SimpleImputer
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
# Remove the id, date and new_cat attribute because median can only be calculated on numerical attributes
housesales_num = housesales.drop(['id','date', 'new_cat'], axis=1)
housesales_num.head()
| bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15949 | 2 | 1.00 | 930.0 | 10505 | 1.0 | 0 | 0 | 3 | 6 | 930 | 0 | 1930 | 0 | 98148 | 47.4337 | -122.329 | 1520 | 8881 |
| 16409 | 2 | 1.00 | 700.0 | 6000 | 1.0 | 0 | 0 | 3 | 6 | 700 | 0 | 1943 | 0 | 98055 | 47.4671 | -122.212 | 1320 | 6000 |
| 14668 | 3 | 1.00 | 1580.0 | 3840 | 2.0 | 0 | 0 | 3 | 8 | 1580 | 0 | 1908 | 0 | 98102 | 47.6192 | -122.319 | 1680 | 2624 |
| 6877 | 3 | 2.25 | 1646.0 | 12414 | 2.0 | 0 | 0 | 3 | 7 | 1646 | 0 | 1996 | 0 | 98038 | 47.3630 | -122.035 | 1654 | 8734 |
| 20213 | 3 | 3.25 | 1450.0 | 1468 | 2.0 | 0 | 0 | 3 | 8 | 1100 | 350 | 2009 | 0 | 98126 | 47.5664 | -122.370 | 1450 | 1478 |
# Fit the Simple Imputer
imputer.fit(housesales_num)
SimpleImputer(copy=True, fill_value=None, missing_values=nan,
strategy='median', verbose=0)
# Query the Simple Imputer statistics
imputer.statistics_
array([ 3.00000e+00, 2.25000e+00, 1.91000e+03, 7.62000e+03,
1.50000e+00, 0.00000e+00, 0.00000e+00, 3.00000e+00,
7.00000e+00, 1.56000e+03, 0.00000e+00, 1.97500e+03,
0.00000e+00, 9.80650e+04, 4.75728e+01, -1.22229e+02,
1.84000e+03, 7.62000e+03])
# Show median by other mean to contrast results
housesales_num.median().values
array([ 3.00000e+00, 2.25000e+00, 1.91000e+03, 7.62000e+03,
1.50000e+00, 0.00000e+00, 0.00000e+00, 3.00000e+00,
7.00000e+00, 1.56000e+03, 0.00000e+00, 1.97500e+03,
0.00000e+00, 9.80650e+04, 4.75728e+01, -1.22229e+02,
1.84000e+03, 7.62000e+03])
# Apply the transformation to create our new X
X = imputer.transform(housesales_num)
# Create a dataframe from X (a numpy array object)
housesales_tr = pd.DataFrame(X, columns=housesales_num.columns,
index = list(housesales.index.values))
# Show that columns containing NaN values are filled out
housesales_tr.loc[incomplete_rows.index.values].head(5)
| bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7517 | 4.0 | 2.00 | 1910.0 | 6375.0 | 2.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1530.0 | 0.0 | 1942.0 | 1983.0 | 98058.0 | 47.4692 | -122.162 | 1500.0 | 8712.0 |
| 5711 | 3.0 | 2.25 | 1910.0 | 17235.0 | 1.0 | 0.0 | 0.0 | 4.0 | 7.0 | 1440.0 | 280.0 | 1974.0 | 0.0 | 98042.0 | 47.3438 | -122.073 | 1990.0 | 35048.0 |
| 20979 | 2.0 | 1.75 | 1910.0 | 1005.0 | 1.5 | 0.0 | 0.0 | 3.0 | 9.0 | 900.0 | 510.0 | 2011.0 | 0.0 | 98027.0 | 47.5446 | -122.018 | 1440.0 | 1188.0 |
| 19431 | 5.0 | 3.25 | 1910.0 | 20790.0 | 1.0 | 0.0 | 0.0 | 4.0 | 7.0 | 1800.0 | 1060.0 | 1965.0 | 0.0 | 98155.0 | 47.7757 | -122.295 | 1920.0 | 9612.0 |
| 10994 | 4.0 | 1.75 | 1910.0 | 6975.0 | 1.0 | 0.0 | 0.0 | 3.0 | 8.0 | 1420.0 | 300.0 | 1975.0 | 0.0 | 98052.0 | 47.6506 | -122.121 | 2210.0 | 7875.0 |
# Query the strategy used
imputer.strategy
'median'
# Create a datafrane by resetting the indexes
housesales_tr = pd.DataFrame(X, columns=housesales_num.columns)
housesales_tr.head()
| bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.0 | 1.00 | 930.0 | 10505.0 | 1.0 | 0.0 | 0.0 | 3.0 | 6.0 | 930.0 | 0.0 | 1930.0 | 0.0 | 98148.0 | 47.4337 | -122.329 | 1520.0 | 8881.0 |
| 1 | 2.0 | 1.00 | 700.0 | 6000.0 | 1.0 | 0.0 | 0.0 | 3.0 | 6.0 | 700.0 | 0.0 | 1943.0 | 0.0 | 98055.0 | 47.4671 | -122.212 | 1320.0 | 6000.0 |
| 2 | 3.0 | 1.00 | 1580.0 | 3840.0 | 2.0 | 0.0 | 0.0 | 3.0 | 8.0 | 1580.0 | 0.0 | 1908.0 | 0.0 | 98102.0 | 47.6192 | -122.319 | 1680.0 | 2624.0 |
| 3 | 3.0 | 2.25 | 1646.0 | 12414.0 | 2.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1646.0 | 0.0 | 1996.0 | 0.0 | 98038.0 | 47.3630 | -122.035 | 1654.0 | 8734.0 |
| 4 | 3.0 | 3.25 | 1450.0 | 1468.0 | 2.0 | 0.0 | 0.0 | 3.0 | 8.0 | 1100.0 | 350.0 | 2009.0 | 0.0 | 98126.0 | 47.5664 | -122.370 | 1450.0 | 1478.0 |
Handling Categorial Attributes
# Show the categorial feature
housesales_cat = housesales['new_cat']
housesales_cat.head(10)
15949 D
16409 D
14668 D
6877 D
20213 B
20729 E
15265 A
18161 D
5309 E
2688 E
Name: new_cat, dtype: object
# (Option 1) Apply Ordinal Encoder to our categorical feature
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housesales_cat_encoded = ordinal_encoder.fit_transform(housesales_cat.values.reshape(-1,1))
housesales_cat_encoded[:10]
array([[3.],
[3.],
[3.],
[3.],
[1.],
[4.],
[0.],
[3.],
[4.],
[4.]])
# Query those categories found
ordinal_encoder.categories_
[array(['A', 'B', 'C', 'D', 'E'], dtype=object)]
# (Option 2) Apply OneHotEnconder to our categorical feature
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housesales_cat_1hot = cat_encoder.fit_transform(housesales_cat.values.reshape(-1,1))
housesales_cat_1hot
<17290x5 sparse matrix of type '<class 'numpy.float64'>'
with 17290 stored elements in Compressed Sparse Row format>
# By default, the OneHotEncoder class returns a sparse array, but we can convert it to a dense array
# if needed by calling the toarray() method
housesales_cat_1hot.toarray()
array([[0., 0., 0., 1., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 1., 0.],
...,
[0., 0., 0., 0., 1.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.]])
# (Option 2B) Alternatively, you can set sparse=False when creating the OneHotEncoder:
cat_encoder = OneHotEncoder(sparse=False)
housesales_cat_1hot = cat_encoder.fit_transform(housesales_cat.values.reshape(-1,1))
housesales_cat_1hot
array([[0., 0., 0., 1., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 1., 0.],
...,
[0., 0., 0., 0., 1.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.]])
# Query those categories found
cat_encoder.categories_
[array(['A', 'B', 'C', 'D', 'E'], dtype=object)]
Custom transformes
# Query what the columns are
housesales.columns
Index(['id', 'date', 'bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot',
'floors', 'waterfront', 'view', 'condition', 'grade', 'sqft_above',
'sqft_basement', 'yr_built', 'yr_renovated', 'zipcode', 'lat', 'long',
'sqft_living15', 'sqft_lot15', 'new_cat'],
dtype='object')
# Show the initial shape
housesales.shape
(17290, 21)
# Create a function to add new features a apply this one
from sklearn.preprocessing import FunctionTransformer
# get the right column indices: safer than hard-coding indices
bedrooms_ix, bathrooms_ix, floors_ix = [
list(housesales.columns).index(col)
for col in ("bedrooms", "bathrooms", "floors")]
def add_extra_features(X, add_bathrooms_per_floors=True):
bedrooms_per_floor = X[:, bedrooms_ix] / X[:, floors_ix]
if add_bathrooms_per_floors:
bathrooms_per_floor = X[:, bathrooms_ix] / X[:, floors_ix]
return np.c_[X, bedrooms_per_floor, bathrooms_per_floor]
else:
return np.c_[X, bedrooms_per_floors]
attr_adder = FunctionTransformer(add_extra_features, validate=False,
kw_args={"add_bathrooms_per_floors": True})
housesales_extra_attribs = attr_adder.fit_transform(housesales.values)
# Query the current dataset's shape
housesales_extra_attribs.shape
(17290, 23)
# Create a dataframe using our dataset with extra attributes
housesales_extra_attribs = pd.DataFrame(
housesales_extra_attribs,
columns=list(housesales.columns)+["bedrooms_per_floor", "bathrooms_per_floor"])
housesales_extra_attribs.head()
| id | date | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | ... | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | new_cat | bedrooms_per_floor | bathrooms_per_floor | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3223049073 | 20150413T000000 | 2 | 1 | 930 | 10505 | 1 | 0 | 0 | 3 | ... | 1930 | 0 | 98148 | 47.4337 | -122.329 | 1520 | 8881 | D | 2 | 1 |
| 1 | 7231600098 | 20141014T000000 | 2 | 1 | 700 | 6000 | 1 | 0 | 0 | 3 | ... | 1943 | 0 | 98055 | 47.4671 | -122.212 | 1320 | 6000 | D | 2 | 1 |
| 2 | 6003500995 | 20140617T000000 | 3 | 1 | 1580 | 3840 | 2 | 0 | 0 | 3 | ... | 1908 | 0 | 98102 | 47.6192 | -122.319 | 1680 | 2624 | D | 1.5 | 0.5 |
| 3 | 9406520290 | 20141229T000000 | 3 | 2.25 | 1646 | 12414 | 2 | 0 | 0 | 3 | ... | 1996 | 0 | 98038 | 47.363 | -122.035 | 1654 | 8734 | D | 1.5 | 1.125 |
| 4 | 9358001403 | 20140903T000000 | 3 | 3.25 | 1450 | 1468 | 2 | 0 | 0 | 3 | ... | 2009 | 0 | 98126 | 47.5664 | -122.37 | 1450 | 1478 | B | 1.5 | 1.625 |
5 rows × 23 columns
Tranformation pipelines
# get the right column indices: safer than hard-coding indices
bedrooms_ix, bathrooms_ix, floors_ix = [
list(housesales_num.columns).index(col)
for col in ("bedrooms", "bathrooms", "floors")]
# Create and apply a pipeline
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', FunctionTransformer(add_extra_features, validate=False)),
('std_scaler', StandardScaler()),
])
housesales_num_tr = num_pipeline.fit_transform(housesales_num)
housesales_num_tr
array([[-1.46672477, -1.44618721, -1.25691191, ..., -0.14296104,
-0.50174116, -0.88035119],
[-1.46672477, -1.44618721, -1.5083036 , ..., -0.24818937,
-0.50174116, -0.88035119],
[-0.39822931, -1.44618721, -0.54645714, ..., -0.37149753,
-0.99708187, -1.75026065],
...,
[ 0.67026615, -0.79817361, -0.54645714, ..., -0.21166443,
1.47962167, -0.01044172],
[-0.39822931, -0.15016001, -0.73226839, ..., -0.20618569,
0.48894025, 0.85946775],
[-1.46672477, -0.15016001, -1.10389088, ..., -0.16819977,
-0.50174116, 0.85946775]])
# Form a full pipeline and apply it
from sklearn.compose import ColumnTransformer
num_attribs = list(housesales_num)
cat_attribs = ["new_cat"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs),
])
housesales_prepared = full_pipeline.fit_transform(housesales)
housesales_prepared
array([[-1.46672477, -1.44618721, -1.25691191, ..., 0. ,
1. , 0. ],
[-1.46672477, -1.44618721, -1.5083036 , ..., 0. ,
1. , 0. ],
[-0.39822931, -1.44618721, -0.54645714, ..., 0. ,
1. , 0. ],
...,
[ 0.67026615, -0.79817361, -0.54645714, ..., 0. ,
0. , 1. ],
[-0.39822931, -0.15016001, -0.73226839, ..., 1. ,
0. , 0. ],
[-1.46672477, -0.15016001, -1.10389088, ..., 0. ,
1. , 0. ]])
# Query the resulting shape
housesales_prepared.shape
(17290, 25)
Select and Train a model
1st Model: Linear Regression
# Select and fit the model
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housesales_prepared, housesales_labels)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
normalize=False)
# Apply the full preprocessing pipeline to a few training instances and make predictions
some_data = housesales.iloc[:5]
some_labels = housesales_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("Predictions:", lin_reg.predict(some_data_prepared))
Predictions: [160246.20608284 132980.36446407 591549.02987724 186586.83900952
424069.28829244]
# Compare against the actual values:
print("Labels:", list(some_labels))
Labels: [235000.0, 225000.0, 729000.0, 305000.0, 380000.0]
# Calculate the root mean square error
from sklearn.metrics import mean_squared_error
housesales_predictions = lin_reg.predict(housesales_prepared)
lin_mse = mean_squared_error(housesales_labels, housesales_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
198780.6337961526
# Calculate the mean absolute error
from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(housesales_labels, housesales_predictions)
lin_mae
125213.23059294488
2nd Model: Decision Tree Regressor
# Pick up and fit the model
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(random_state=10)
tree_reg.fit(housesales_prepared, housesales_labels)
DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=10, splitter='best')
# Calculate the root mean square error
housesales_predictions = tree_reg.predict(housesales_prepared)
tree_mse = mean_squared_error(housesales_labels, housesales_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
4490.00962109037
3rd Model: Random Forest Regressor
# Pick up and fit the model
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=10, random_state=10)
forest_reg.fit(housesales_prepared, housesales_labels)
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None,
oob_score=False, random_state=10, verbose=0, warm_start=False)
# Calculate the root mean square error
housesales_predictions = forest_reg.predict(housesales_prepared)
forest_mse = mean_squared_error(housesales_labels, housesales_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
56955.76782837187
# Show the three performance results
round(lin_rmse,2), round(tree_rmse,2), round(forest_rmse,2)
(198780.63, 4490.01, 56955.77)
Evaluation Using Cross-Validation
# Apply cross-validation to tree regression
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housesales_prepared, housesales_labels,
scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores)
def display_scores(scores):
print("Scores:", scores)
print("Mean:", scores.mean())
print("Standard deviation:", scores.std())
display_scores(tree_rmse_scores)
Scores: [173778.94629228 175710.89013465 187176.67519944 180469.08500644
188418.63291527 201853.73211207 171094.25938394 215862.78771941
191758.00742614 193737.92316176]
Mean: 187986.09393513983
Standard deviation: 13084.10384654563
# Apply cross-validation to linear regression
lin_scores = cross_val_score(lin_reg, housesales_prepared, housesales_labels,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
Scores: [185493.6500498 188143.28719886 196526.07710998 208534.84844644
215046.76635923 211968.71458098 185051.93697053 186166.1492152
222359.5286886 192915.03297193]
Mean: 199220.599159155
Standard deviation: 13283.348795742313
# Apply cross-validation Random Forest Regression
from sklearn.model_selection import cross_val_score
forest_scores = cross_val_score(forest_reg, housesales_prepared, housesales_labels,
scoring="neg_mean_squared_error", cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
Scores: [125914.66829472 121179.48032379 131031.06602869 140348.49069738
136853.08186766 138409.66704917 122564.43056517 151594.7942008
158434.65537147 145115.11660802]
Mean: 137144.54510068757
Standard deviation: 11698.320601431275
Fine-tune using grid search
# Search for the the best pair of hyperparameters
from sklearn.model_selection import GridSearchCV
param_grid = [
# try 12 (3×4) combinations of hyperparameters
{'n_estimators': [3, 10, 30], 'max_features': [4, 8, 12, 16]},
# then try 6 (2×3) combinations with bootstrap set as False
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [4, 8, 12]},
]
forest_reg = RandomForestRegressor(random_state=10)
# train across 5 folds, that's a total of (12+6)*5=90 rounds of training
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error', return_train_score=True)
grid_search.fit(housesales_prepared, housesales_labels)
GridSearchCV(cv=5, error_score='raise-deprecating',
estimator=RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators='warn', n_jobs=None,
oob_score=False, random_state=10, verbose=0, warm_start=False),
fit_params=None, iid='warn', n_jobs=None,
param_grid=[{'n_estimators': [3, 10, 30], 'max_features': [4, 8, 12, 16]}, {'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [4, 8, 12]}],
pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
scoring='neg_mean_squared_error', verbose=0)
# Print the best parameters obtained
grid_search.best_params_
{'max_features': 16, 'n_estimators': 30}
# Show the best estimator obtained
grid_search.best_estimator_
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features=16, max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=30, n_jobs=None, oob_score=False, random_state=10,
verbose=0, warm_start=False)
# Print all results obtained
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
175766.9960307246 {'max_features': 4, 'n_estimators': 3}
149998.47472561774 {'max_features': 4, 'n_estimators': 10}
141431.3612920264 {'max_features': 4, 'n_estimators': 30}
162014.7744711493 {'max_features': 8, 'n_estimators': 3}
141138.59199611377 {'max_features': 8, 'n_estimators': 10}
134723.96819813742 {'max_features': 8, 'n_estimators': 30}
157713.3917482858 {'max_features': 12, 'n_estimators': 3}
138557.65222266223 {'max_features': 12, 'n_estimators': 10}
133762.08340063755 {'max_features': 12, 'n_estimators': 30}
152564.4040221663 {'max_features': 16, 'n_estimators': 3}
135830.7709838851 {'max_features': 16, 'n_estimators': 10}
131391.92055126876 {'max_features': 16, 'n_estimators': 30}
163409.15856683112 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3}
142366.60188169198 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10}
160971.30667826644 {'bootstrap': False, 'max_features': 8, 'n_estimators': 3}
135633.3762699063 {'bootstrap': False, 'max_features': 8, 'n_estimators': 10}
157801.14473538313 {'bootstrap': False, 'max_features': 12, 'n_estimators': 3}
134312.77415365016 {'bootstrap': False, 'max_features': 12, 'n_estimators': 10}
pd.DataFrame(grid_search.cv_results_)
| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_max_features | param_n_estimators | param_bootstrap | params | split0_test_score | split1_test_score | ... | mean_test_score | std_test_score | rank_test_score | split0_train_score | split1_train_score | split2_train_score | split3_train_score | split4_train_score | mean_train_score | std_train_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.094308 | 0.011228 | 0.001405 | 0.001749 | 4 | 3 | NaN | {'max_features': 4, 'n_estimators': 3} | -2.727283e+10 | -3.261322e+10 | ... | -3.089404e+10 | 1.883519e+09 | 18 | -8.817919e+09 | -8.438907e+09 | -8.180504e+09 | -8.752257e+09 | -8.833278e+09 | -8.604573e+09 | 2.557001e+08 |
| 1 | 0.293464 | 0.007064 | 0.010466 | 0.005718 | 4 | 10 | NaN | {'max_features': 4, 'n_estimators': 10} | -1.792067e+10 | -2.287644e+10 | ... | -2.249954e+10 | 2.768489e+09 | 11 | -4.403258e+09 | -3.999802e+09 | -4.085513e+09 | -3.877427e+09 | -4.167194e+09 | -4.106639e+09 | 1.766626e+08 |
| 2 | 0.913985 | 0.041151 | 0.028847 | 0.003409 | 4 | 30 | NaN | {'max_features': 4, 'n_estimators': 30} | -1.593909e+10 | -2.100100e+10 | ... | -2.000283e+10 | 2.606794e+09 | 9 | -3.206317e+09 | -3.114663e+09 | -3.010621e+09 | -3.085097e+09 | -3.090956e+09 | -3.101531e+09 | 6.292702e+07 |
| 3 | 0.143824 | 0.007881 | 0.000801 | 0.001602 | 8 | 3 | NaN | {'max_features': 8, 'n_estimators': 3} | -2.182884e+10 | -2.623712e+10 | ... | -2.624879e+10 | 2.386585e+09 | 16 | -7.585095e+09 | -7.184938e+09 | -8.175218e+09 | -6.878654e+09 | -7.269957e+09 | -7.418772e+09 | 4.400968e+08 |
| 4 | 0.522798 | 0.024371 | 0.010616 | 0.000794 | 8 | 10 | NaN | {'max_features': 8, 'n_estimators': 10} | -1.601112e+10 | -2.047524e+10 | ... | -1.992010e+10 | 2.008897e+09 | 8 | -3.824747e+09 | -3.670972e+09 | -3.851233e+09 | -3.461211e+09 | -3.576312e+09 | -3.676895e+09 | 1.475979e+08 |
| 5 | 1.471522 | 0.024280 | 0.027677 | 0.006078 | 8 | 30 | NaN | {'max_features': 8, 'n_estimators': 30} | -1.472139e+10 | -1.812115e+10 | ... | -1.815055e+10 | 2.185784e+09 | 4 | -2.853716e+09 | -2.730984e+09 | -2.945123e+09 | -2.758021e+09 | -2.748576e+09 | -2.807284e+09 | 8.105632e+07 |
| 6 | 0.215546 | 0.018990 | 0.004924 | 0.005718 | 12 | 3 | NaN | {'max_features': 12, 'n_estimators': 3} | -2.162281e+10 | -2.263662e+10 | ... | -2.487351e+10 | 2.463542e+09 | 13 | -7.866118e+09 | -6.996194e+09 | -6.822348e+09 | -7.655889e+09 | -7.427087e+09 | -7.353527e+09 | 3.922809e+08 |
| 7 | 0.701556 | 0.011628 | 0.009934 | 0.005323 | 12 | 10 | NaN | {'max_features': 12, 'n_estimators': 10} | -1.587845e+10 | -1.822873e+10 | ... | -1.919822e+10 | 2.023721e+09 | 7 | -3.873012e+09 | -3.583551e+09 | -3.889845e+09 | -3.743148e+09 | -3.842905e+09 | -3.786492e+09 | 1.135022e+08 |
| 8 | 2.058677 | 0.034632 | 0.028129 | 0.006240 | 12 | 30 | NaN | {'max_features': 12, 'n_estimators': 30} | -1.511352e+10 | -1.727709e+10 | ... | -1.789229e+10 | 1.668174e+09 | 2 | -2.864978e+09 | -2.641198e+09 | -2.795556e+09 | -2.791882e+09 | -2.750623e+09 | -2.768847e+09 | 7.363643e+07 |
| 9 | 0.262557 | 0.007748 | 0.002828 | 0.001475 | 16 | 3 | NaN | {'max_features': 16, 'n_estimators': 3} | -2.027329e+10 | -2.286520e+10 | ... | -2.327590e+10 | 1.638003e+09 | 12 | -6.559394e+09 | -6.289101e+09 | -6.736163e+09 | -6.907248e+09 | -6.577818e+09 | -6.613945e+09 | 2.053135e+08 |
| 10 | 0.876025 | 0.027222 | 0.010639 | 0.008989 | 16 | 10 | NaN | {'max_features': 16, 'n_estimators': 10} | -1.605120e+10 | -1.785551e+10 | ... | -1.845000e+10 | 1.376784e+09 | 6 | -3.672691e+09 | -3.311100e+09 | -3.732889e+09 | -3.411158e+09 | -3.223571e+09 | -3.470282e+09 | 1.998162e+08 |
| 11 | 2.593708 | 0.036903 | 0.031253 | 0.000012 | 16 | 30 | NaN | {'max_features': 16, 'n_estimators': 30} | -1.491269e+10 | -1.649109e+10 | ... | -1.726384e+10 | 1.403249e+09 | 1 | -2.738781e+09 | -2.502196e+09 | -2.902519e+09 | -2.600639e+09 | -2.542216e+09 | -2.657270e+09 | 1.464810e+08 |
| 12 | 0.138856 | 0.003547 | 0.009381 | 0.007659 | 4 | 3 | False | {'bootstrap': False, 'max_features': 4, 'n_est... | -2.258436e+10 | -2.847454e+10 | ... | -2.670255e+10 | 3.502579e+09 | 17 | -1.358209e+07 | -7.133046e+06 | -2.213945e+07 | -2.260459e+07 | -1.459475e+07 | -1.601079e+07 | 5.792353e+06 |
| 13 | 0.449354 | 0.020148 | 0.012495 | 0.006248 | 4 | 10 | False | {'bootstrap': False, 'max_features': 4, 'n_est... | -1.701797e+10 | -2.030765e+10 | ... | -2.026825e+10 | 2.014312e+09 | 10 | -1.358564e+07 | -7.135718e+06 | -2.213989e+07 | -2.260240e+07 | -1.454593e+07 | -1.600191e+07 | 5.793251e+06 |
| 14 | 0.230184 | 0.005129 | 0.003130 | 0.006259 | 8 | 3 | False | {'bootstrap': False, 'max_features': 8, 'n_est... | -2.268334e+10 | -2.514249e+10 | ... | -2.591176e+10 | 3.437098e+09 | 15 | -1.358163e+07 | -7.132645e+06 | -2.214033e+07 | -2.260194e+07 | -1.453739e+07 | -1.599879e+07 | 5.794947e+06 |
| 15 | 0.766779 | 0.014362 | 0.011012 | 0.006225 | 8 | 10 | False | {'bootstrap': False, 'max_features': 8, 'n_est... | -1.577869e+10 | -1.711504e+10 | ... | -1.839641e+10 | 1.788955e+09 | 5 | -1.358291e+07 | -7.132681e+06 | -2.213887e+07 | -2.260202e+07 | -1.453743e+07 | -1.599878e+07 | 5.794536e+06 |
| 16 | 0.312679 | 0.006287 | 0.003126 | 0.006251 | 12 | 3 | False | {'bootstrap': False, 'max_features': 12, 'n_es... | -2.191600e+10 | -2.428039e+10 | ... | -2.490120e+10 | 1.829720e+09 | 14 | -1.358163e+07 | -7.132645e+06 | -2.213913e+07 | -2.260194e+07 | -1.453842e+07 | -1.599875e+07 | 5.794640e+06 |
| 17 | 1.096888 | 0.015974 | 0.018734 | 0.003809 | 12 | 10 | False | {'bootstrap': False, 'max_features': 12, 'n_es... | -1.554204e+10 | -1.818778e+10 | ... | -1.803992e+10 | 1.297051e+09 | 3 | -1.358163e+07 | -7.132645e+06 | -2.213887e+07 | -2.260194e+07 | -1.453752e+07 | -1.599852e+07 | 5.794631e+06 |
18 rows × 23 columns
Fine-tune using Randomized Search
# Search for best hyperparameters using ranges
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_distribs = {
'n_estimators': randint(low=1, high=200),
'max_features': randint(low=1, high=16),
}
forest_reg = RandomForestRegressor(random_state=10)
rnd_search = RandomizedSearchCV(forest_reg, param_distributions=param_distribs,
n_iter=10, cv=5, scoring='neg_mean_squared_error', random_state=10)
rnd_search.fit(housesales_prepared, housesales_labels)
RandomizedSearchCV(cv=5, error_score='raise-deprecating',
estimator=RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators='warn', n_jobs=None,
oob_score=False, random_state=10, verbose=0, warm_start=False),
fit_params=None, iid='warn', n_iter=10, n_jobs=None,
param_distributions={'n_estimators': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000003ABAC15518>, 'max_features': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000003ABAC21748>},
pre_dispatch='2*n_jobs', random_state=10, refit=True,
return_train_score='warn', scoring='neg_mean_squared_error',
verbose=0)
# Show results obtained
cvres = rnd_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
129532.52730078508 {'max_features': 10, 'n_estimators': 126}
140169.5236721647 {'max_features': 5, 'n_estimators': 16}
168763.4353289947 {'max_features': 1, 'n_estimators': 114}
129100.61994092652 {'max_features': 12, 'n_estimators': 157}
129316.18397875247 {'max_features': 10, 'n_estimators': 158}
163284.03368410614 {'max_features': 2, 'n_estimators': 9}
215431.99623720883 {'max_features': 10, 'n_estimators': 1}
131772.39271442383 {'max_features': 11, 'n_estimators': 41}
131011.30449087144 {'max_features': 7, 'n_estimators': 165}
145105.1193332708 {'max_features': 4, 'n_estimators': 17}
# Show importance of features
feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances
array([0.0022996 , 0.01254997, 0.222924 , 0.01515698, 0.00152163,
0.02171765, 0.01642199, 0.00257684, 0.30979218, 0.03223202,
0.00614749, 0.0334077 , 0.0017791 , 0.01711046, 0.14800092,
0.06551846, 0.05948528, 0.01370116, 0.00357358, 0.00747337,
0.00090465, 0.0010297 , 0.0010995 , 0.00132694, 0.00224884])
# Show features from most importance to least importance
extra_attribs = ["bedrooms_per_floor", "bathrooms_per_floor"]
cat_encoder = full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)
[(0.3097921838147633, 'grade'),
(0.22292399910753496, 'sqft_living'),
(0.1480009225542765, 'lat'),
(0.06551845815073715, 'long'),
(0.0594852835256222, 'sqft_living15'),
(0.033407700475521135, 'yr_built'),
(0.03223201629067148, 'sqft_above'),
(0.021717654073000706, 'waterfront'),
(0.017110455391059758, 'zipcode'),
(0.01642198830109303, 'view'),
(0.015156976947906724, 'sqft_lot'),
(0.013701156535242382, 'sqft_lot15'),
(0.01254997183928799, 'bathrooms'),
(0.007473372451509992, 'bathrooms_per_floor'),
(0.0061474868639639696, 'sqft_basement'),
(0.0035735813028082266, 'bedrooms_per_floor'),
(0.0025768396837983916, 'condition'),
(0.002299595929279424, 'bedrooms'),
(0.002248841241609929, 'E'),
(0.0017790999438058127, 'yr_renovated'),
(0.0015216328773221272, 'floors'),
(0.001326936997394509, 'D'),
(0.0010995043091287236, 'C'),
(0.0010296962093261552, 'B'),
(0.0009046451833354189, 'A')]
Evaluate the best model on the Test set
# Take the best estimator and calculate the RMSE on test data
final_model = grid_search.best_estimator_
X_test = test_set.drop("price", axis=1)
y_test = test_set["price"].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse
132428.4777030345
References
- Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems