Linear Support Vector Machine Classiffier 08 Apr 2019
This notebook ilustrates how to use linear support vector machine for a binary classification task. We will be using the “wine” dataset provided by the Scikit-learn library.
Initial Setup
This cell contains common imports that we will be using through this notebook.
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
Load Data
As we have mentioned, we will be using the wine dataset. Let’s load this dataset and show its description.
from sklearn import datasets
wine = datasets.load_wine()
list(wine.keys())
['data', 'target', 'target_names', 'DESCR', 'feature_names']
print(wine.DESCR)
.. _wine_dataset:
Wine recognition dataset
------------------------
**Data Set Characteristics:**
:Number of Instances: 178 (50 in each of three classes)
:Number of Attributes: 13 numeric, predictive attributes and the class
:Attribute Information:
- Alcohol
- Malic acid
- Ash
- Alcalinity of ash
- Magnesium
- Total phenols
- Flavanoids
- Nonflavanoid phenols
- Proanthocyanins
- Color intensity
- Hue
- OD280/OD315 of diluted wines
- Proline
- class:
- class_0
- class_1
- class_2
:Summary Statistics:
============================= ==== ===== ======= =====
Min Max Mean SD
============================= ==== ===== ======= =====
Alcohol: 11.0 14.8 13.0 0.8
Malic Acid: 0.74 5.80 2.34 1.12
Ash: 1.36 3.23 2.36 0.27
Alcalinity of Ash: 10.6 30.0 19.5 3.3
Magnesium: 70.0 162.0 99.7 14.3
Total Phenols: 0.98 3.88 2.29 0.63
Flavanoids: 0.34 5.08 2.03 1.00
Nonflavanoid Phenols: 0.13 0.66 0.36 0.12
Proanthocyanins: 0.41 3.58 1.59 0.57
Colour Intensity: 1.3 13.0 5.1 2.3
Hue: 0.48 1.71 0.96 0.23
OD280/OD315 of diluted wines: 1.27 4.00 2.61 0.71
Proline: 278 1680 746 315
============================= ==== ===== ======= =====
:Missing Attribute Values: None
:Class Distribution: class_0 (59), class_1 (71), class_2 (48)
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
This is a copy of UCI ML Wine recognition datasets.
https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data
The data is the results of a chemical analysis of wines grown in the same
region in Italy by three different cultivators. There are thirteen different
measurements taken for different constituents found in the three types of
wine.
Original Owners:
Forina, M. et al, PARVUS -
An Extendible Package for Data Exploration, Classification and Correlation.
Institute of Pharmaceutical and Food Analysis and Technologies,
Via Brigata Salerno, 16147 Genoa, Italy.
Citation:
Lichman, M. (2013). UCI Machine Learning Repository
[http://archive.ics.uci.edu/ml]. Irvine, CA: University of California,
School of Information and Computer Science.
.. topic:: References
(1) S. Aeberhard, D. Coomans and O. de Vel,
Comparison of Classifiers in High Dimensional Settings,
Tech. Rep. no. 92-02, (1992), Dept. of Computer Science and Dept. of
Mathematics and Statistics, James Cook University of North Queensland.
(Also submitted to Technometrics).
The data was used with many others for comparing various
classifiers. The classes are separable, though only RDA
has achieved 100% correct classification.
(RDA : 100%, QDA 99.4%, LDA 98.9%, 1NN 96.1% (z-transformed data))
(All results using the leave-one-out technique)
(2) S. Aeberhard, D. Coomans and O. de Vel,
"THE CLASSIFICATION PERFORMANCE OF RDA"
Tech. Rep. no. 92-01, (1992), Dept. of Computer Science and Dept. of
Mathematics and Statistics, James Cook University of North Queensland.
(Also submitted to Journal of Chemometrics).
Setting up the binary classification task
As we see, our wine dataset has a classification among 3 classes(class_0, class_1, class_2). Also, it contains 13 features from the “Alcohol” to the “Proline” feature. Since our first task is to work on a binary classification, we pick up two of the three classes. We also pick up just two features so that we can visualize linear boundaries between the two classes once we train our model.
X = wine["data"][:, (9, 1)] # Color intensity, Malic acid
y = wine["target"]
class_2_or_class_1 = (y == 2) | (y == 1)
X = X[class_2_or_class_1]
y = y[class_2_or_class_1]
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Class_1")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "yo", label="Class_2")
plt.xlabel("Color Intensity", fontsize=14)
plt.ylabel("Malic Acid", fontsize=14)
plt.legend(loc="upper right", fontsize=14)
plt.axis([0, 13, 0, 5.9])
[0, 13, 0, 5.9]
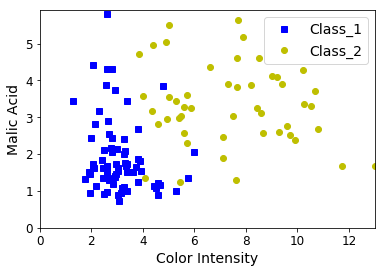
As we see, our dataset is not linearly separable. Any line we can consider to separate these two classes will make some violations. When the dataset is not linearly separable, it is said that we are dealing with a soft margin classification.
Linear SVM Classifier
Once dataset is ready, we can fit the Linear SVM(Support Vector Machine) model. We consider a C parameter that regulates the cost of allowing a point on the wrong site. If C is small, it is fine to misclassify. Is C is large, we penalize high each missclassification. The value of C affects the margin of the linear SVM as we will see.
from sklearn.svm import SVC
# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float(10**6))
svm_clf.fit(X, y)
SVC(C=1000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)
Once the linear SVM model has been trained, we can plot the linear classifier obtained as well as the margin obtained by this model for the specific paramater C. Also, we can compare the linear SVM classifier obtained with other random “bad” linear classifiers.
# Random bad models
x0 = np.linspace(0, 13, 200)
pred_1 = 5*x0 - 20
pred_2 = -.75 * x0 + 6.6
pred_3 = -3.0 * x0 + 15.5
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# At the decision boundary, w0*x0 + w1*x1 + b = 0
# => x1 = -w0/w1 * x0 - b/w1
x0 = np.linspace(xmin, xmax, 200)
decision_boundary = -w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=360, facecolors='#FFAAAA')
plt.plot(x0, decision_boundary, "k-", linewidth=2)
plt.plot(x0, gutter_up, "k--", linewidth=2)
plt.plot(x0, gutter_down, "k--", linewidth=2)
plt.figure(figsize=(12,12))
plt.subplot(211)
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Class_1")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "yo", label="Class_2")
plt.xlabel("Color Intensity", fontsize=14)
plt.ylabel("Malic Acid", fontsize=14)
plt.legend(loc="upper right", fontsize=14)
plt.axis([0, 13, 0, 5.9])
plt.subplot(212)
plot_svc_decision_boundary(svm_clf, 0, 13)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "yo")
plt.xlabel("Color Intensity", fontsize=14)
plt.ylabel("Malic Acid", fontsize=14)
plt.axis([0, 13, 0, 5.9])
plt.show()
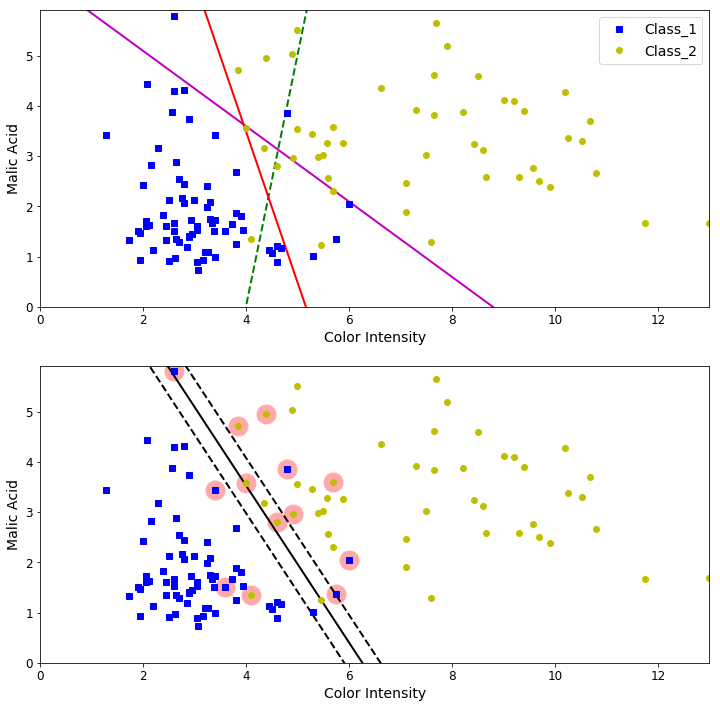
Data points that are circled are named Support Vectors. It turns out that these vectors “support” the linear SVM solution. We can make predictions using our trained model.
svm_clf.predict([[5, 3]])
array([2])
Sensitivity to feature scales
Feature scaling is a common practice that helps to improve the performance of a SVM model by reducing the sensitivity.
Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(Xs[:, 0][ys==1], Xs[:, 1][ys==1], "bo")
plt.plot(Xs[:, 0][ys==0], Xs[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$ ", fontsize=20, rotation=0)
plt.title("Unscaled", fontsize=16)
plt.axis([0, 6, 0, 90])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)
plt.subplot(122)
plt.plot(X_scaled[:, 0][ys==1], X_scaled[:, 1][ys==1], "bo")
plt.plot(X_scaled[:, 0][ys==0], X_scaled[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x_0$", fontsize=20)
plt.title("Scaled", fontsize=16)
plt.axis([-2, 2, -2, 2])
[-2, 2, -2, 2]
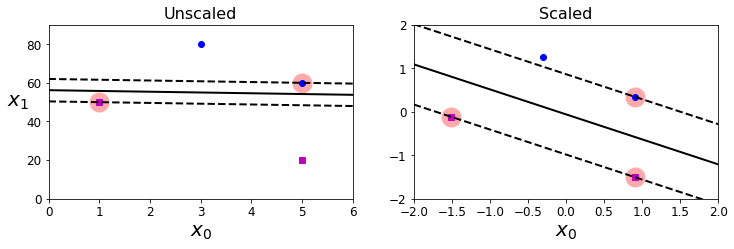
Applying feature scaling to linear SVM
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
wine = datasets.load_wine()
X = wine["data"][:, (9, 1)] # Color intensity, Malic acid
y = wine["target"]
class_2_or_class_1 = (y == 2) | (y == 1)
X = X[class_2_or_class_1]
y = y[class_2_or_class_1]
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge", random_state=10)),
])
svm_clf.fit(X, y)
Pipeline(memory=None,
steps=[('scaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('linear_svc', LinearSVC(C=1, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='hinge', max_iter=1000, multi_class='ovr',
penalty='l2', random_state=10, tol=0.0001, verbose=0))])
To make predictions, we proceed similar to the previous model. The pipeline will take care of scaling our new input.
svm_clf.predict([[5, 3]])
array([2])
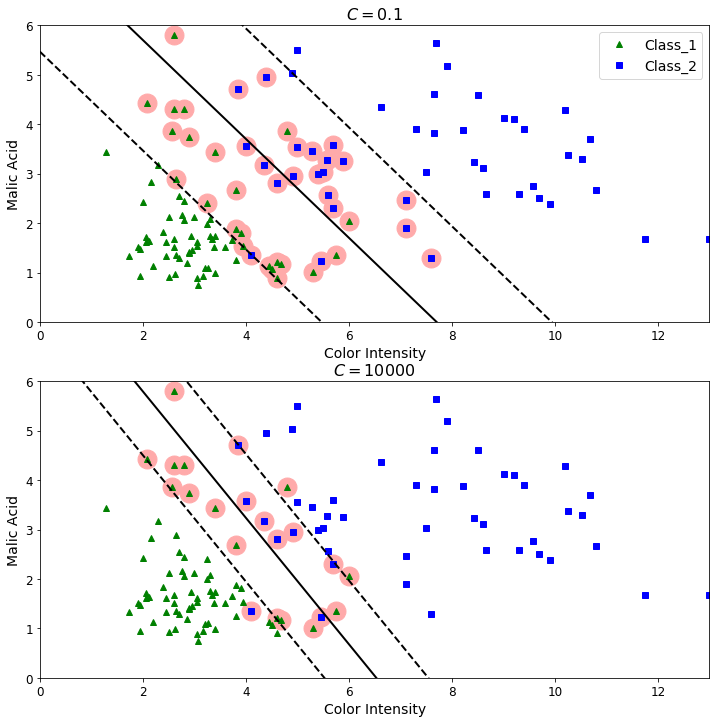
The effect of the parameter C on fitting the model
Now, we will train two linear SVM models for two different parameters C. A smaller C implies a model less sensititive to outliers or change of the dataset. A huge C implies a model more sensitive to change of the dataset.
scaler = StandardScaler()
svm_clf1 = LinearSVC(C=0.1, loss="hinge", random_state=10)
svm_clf2 = LinearSVC(C=10**4, loss="hinge", random_state=10)
scaled_svm_clf1 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf1),
])
scaled_svm_clf2 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf2),
])
scaled_svm_clf1.fit(X, y)
scaled_svm_clf2.fit(X, y)
C:\jcabelloc\Programs\Anaconda3\lib\site-packages\sklearn\svm\base.py:922: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
"the number of iterations.", ConvergenceWarning)
Pipeline(memory=None,
steps=[('scaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('linear_svc', LinearSVC(C=10000, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='hinge', max_iter=1000, multi_class='ovr',
penalty='l2', random_state=10, tol=0.0001, verbose=0))])
# Convert to unscaled parameters
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
# Find support vectors (LinearSVC does not do this automatically)
t = y*2 - 3
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
support_vectors_idx2 = (t * (X.dot(w2) + b2) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
svm_clf2.support_vectors_ = X[support_vectors_idx2]
plt.figure(figsize=(12,12))
plt.subplot(211)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Class_1")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "bs", label="Class_2")
plot_svc_decision_boundary(svm_clf1, 0, 13)
plt.xlabel("Color Intensity", fontsize=14)
plt.ylabel("Malic Acid", fontsize=14)
plt.legend(loc="upper right", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([0, 13, 0., 6])
plt.subplot(212)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "bs")
plot_svc_decision_boundary(svm_clf2, 0, 13)
plt.xlabel("Color Intensity", fontsize=14)
plt.ylabel("Malic Acid", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([0, 13, 0, 6])
[0, 13, 0, 6]
References
Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems